Patents’ “Self-Consistency” Question: Diversion and Blocking Under a Patent-Racing Model
Introduction
The United States patent system is commonly justified by its provision of economic incentives for innovation.[1] But this justification comes with constant concern that the social benefits of innovation that the patent system stimulates might not outweigh the sum of the system’s various social costs, including potential deadweight loss associated with supracompetitive prices,[2] interference with later-stage innovation,[3] and administrative costs.[4] Consequently, courts have characterized the patent system as incorporating a variety of doctrines and limitations, including multiple requirements for patentability, that achieve a “delicate balance . . . between inventors, who rely on the promise of the law to bring the invention forth, and the public, which should be encouraged to pursue innovations, creations, and new ideas beyond the inventor’s exclusive rights.”[5] Ostensibly, such doctrines and limitations help to manage, in Thomas Jefferson’s words, “the difficulty of drawing a line between the things which are worth to the public the embarrassment of an exclusive patent, and those which are not.”[6]
Notably, however, the patent system’s requirements for patentability largely focus on concerns substantially divorced from assessment of whether a claimed invention contributes anything of significant social value as opposed to something technologically distinctive.[7] Moreover, even as requirements of technological distinctiveness, the standards for obtaining nationwide and more than decade-long rights to exclude others from making, using, or selling the claimed invention[8] are in many ways remarkably low.[9] The lowness of these standards straightforwardly suggests questions about the extent to which the patent system is worth its costs. Further, even if one assumes that the patent system as a whole adds social value, one could worry that low patentability standards substantially impede the system’s overall performance either (1) by leading to patents on “lower-level” innovation that impose costs or active blocks to “higher-level” innovation or (2) by diverting effort from higher-level innovation into lower-level innovation by making lower-level innovation, relatively speaking, overly attractive. For purposes of this Essay, I characterize the first concern as a “blocking” concern and the second concern as a “diversion” concern.
This Essay uses a two-tiered patent-racing model, involving a higher‑level innovation race and a lower-level innovation race to investigate these concerns under circumstances that substantially accord with the patent system’s utilitarian assumptions. By investigating the extent to which a low‑patentability standard patent system undercuts its own goals of promoting dynamic efficiency, the approach here might be viewed as conducting a sort of “self-consistency” test for how well the system operates. Perhaps the most significant conclusion is that, under the two-tiered patent-racing model developed here, intra-system diversion concerns are substantially bounded: there is a likelihood of some diversion to lower-level innovation under various circumstances, but this diversion is sometimes socially desirable and, more generally, is of reasonably limited extent. In contrast, for cumulative‑innovation contexts,[10] patent-blocking concerns are not so well contained within the operation of the model. To this extent, the patent-racing model provides support for recent efforts to use tailoring of patent remedies and tightening of subject-matter eligibility standards to help limit the risk of disproportionate blocking or taxation from relatively low-level innovation, although there remains a question of whether such concerns would be better addressed by raising patentability standards.
This Essay proceeds as follows. Part I provides a primer on patent law and the facial disjunction between patentability standards and conventional wisdom about patent law’s economic rationale. Part II develops a patent‑racing model for innovation and uses it to explore possibilities for higher‑level innovation blocking or for socially undesirable diversion of effort toward lower-level innovation. The Conclusion further discusses the results of Part II and considers implications.
I. Doctrinal Background
United States patents confer rights to exclude others from activities such as making, using, offering to sell, or selling the patented invention in the United States, and these rights last up to twenty years from the associated patent application’s effective filing date[11]—or somewhat longer if a patent term extension is granted.[12] Many patents turn out to have little commercial value,[13] but others are used to secure returns that can amount to billions of dollars.[14]
Even patents that apparently have little positive value can impose costs on a variety of parties—not only administrative costs such as those incurred by the Patent and Trademark Office (PTO),[15] but also patent clearance costs incurred by private parties in attempting to review and clear potentially problematic patent rights before undertaking commercial projects.[16] Indeed, in a world in which the United States alone issues more than 300,000 new (rather than merely reissued) patents each year[17] and there are more than 10 million unexpired patents worldwide,[18] firms can reasonably judge clearance costs too costly to undertake, with this judgment predictably leading to abandoned projects or a greater likelihood of later, resource-intensive patent litigation.[19]
Thus, from a general social welfare standpoint or, more particularly, from a perspective focused on patent law’s constitutionally stated purpose “[t]o promote the Progress of Science and useful Arts,”[20] there is good reason to try to avoid granting patents that do not promise value for the public that counterbalances the social costs that they predictably inflict. To the extent modern patent law seeks to police this line, it substantially does so through enforcement of multiple requirements for patentability: utility, novelty, nonobviousness, restriction of patent claim scope to patentable subject matter, and a requirement that the patent adequately disclose aspects of the asserted technological advance and of the patent’s intended scope.[21]
But these requirements do relatively little to ensure that a patent adds substantial social value. A claimed invention need not function better than any pre-existing technology—or otherwise be viewed as substantially likely to generate significant social benefit—in order to satisfy the utility requirement.[22] Patent law makes a point of not requiring a would-be patentee to build a better mousetrap. Novelty is only lacking if a single prior art reference (e.g., an already-issued patent or a published article in a scientific journal) discloses all elements of the claimed invention arranged as required by the relevant patent claim.[23] The fact that an invention is adequately disclosed adds no requirement that it has substantial social value.[24] Decisions on whether a claimed invention satisfies the requirement of restriction to patentable subject matter can involve judgments about the substantiality of an alleged technological advance, but the test of patentable subject matters is generally understood to involve only a limited, threshold inquiry into the technological character of the claimed invention.[25]
These circumstances leave patent law’s nonobviousness requirement as the primary doctrinal guarantor that, in exchange for potentially privately lucrative but socially costly patent rights, a patent applicant adequately discloses to the public a technological advance that is pertinently substantial. The wisdom of relying so fundamentally on nonobviousness for this gatekeeping role is questionable, however. After all, calling something “nonobvious” might be considered faint praise, and one of the drafters of the Patent Act of 1952, the first version of the Patent Act that explicitly recognized a nonobviousness requirement, made clear that he viewed enactment of the nonobviousness requirement as a means to replace court application of a requirement of “invention” that he found to be too unpredictable and demanding.[26] Although nonobviousness demands more than novelty, nonobviousness still only demands technological distinction from the prior art, not that this distinction either have added or be expected to add to social welfare.[27] Nonetheless, the nonobviousness requirement is the basic tool that patent law has to enforce invention substantiality.
The result is that United States patent law does virtually nothing directly to ensure that patents generate more social value than costs. Moreover, the relatively low demands imposed by the requirements for patentability help ensure that there is a significant question about the extent to which the availability of patents on relatively low-level innovation discourages or impedes the pursuit of higher-level innovation. The next Part uses a patent‑racing model to explore the extent to which a patent system that permits patents on lower-level innovation as well as higher-level innovation is likely to act against its own apparent purpose to promote progress by diverting effort to lower-level innovation or by generating lower-level innovation taxes or blocks on higher-level innovation.
II. Diversion and Blocking Under a Patent-Racing Model
This Part uses a patent-racing model to explore the diversion and blocking concerns highlighted in the Introduction. Such models, long “the darling of patent economists and game theorists,” posit a situation in which patents enable a competitor to use the patent system to secure an exclusive prize for developing an innovation.[28]
A. Model for a Symmetric Patent Race
To analyze effects of patentability standards on likelihood of timely innovation, I consider a racing model in which there is an expected reward for winning the race to develop an innovation and this reward helps determine the number of entrants into the race. Potential entrants into an innovation race are assumed to be risk-neutral rational profit maximizers who are symmetric in their capabilities and prospects. Generally speaking, greater rewards are expected to lead to greater numbers of entrants. In turn, a greater number of entrants is assumed to lead to a greater probability of developing the relevant innovation within a given period of time. The relevant social goal is assumed to be maximizing social welfare, and achievement of this goal is assumed to be advanced by maximizing the probability of developing the innovation.
An entrant decides whether to enter a particular race to develop an innovation based on whether the potential entrant’s expected benefit from participating in the race exceeds the cost of the potential entrant’s participation in the race. For simplicity, an entrant is assumed to gain nothing from participating in the race if the entrant does not win the race,[29] and each potential entrant is assumed to have the same cost for participating in the race.[30] Once in the race, entrants have equal chances of winning, where winning means that the entrant is the first to develop the patentable innovation in question.[31] Further, the overall chance that someone will successfully develop and patent the innovation can increase as the number of entrants rises. For example, the probability of an innovation being developed might be 25% with one entrant in the race but 30% if there is also a second entrant in the race.
This model’s mathematical presentation uses the following parameters:
- V is the private value of winning the race to the winner of the race.
- k is an integer greater than or equal to 1 that is associated with a potential entrant (“the kth potential entrant”).
- C = f∙V is the cost to an entrant of participating in the innovation race, with f being a non-negative real number that can generally be understood to be between 0 and 1 for any innovation that might be developed.[32]
- Pk is the overall probability of the relevant innovation’s being developed by at least one race entrant when there are k race entrants, with P0 = 0 (i.e., there is no probability of producing the innovation if the number of entrants is zero) and
Pk = MIN{[γ + k∙Δ], 1} for k ≥ 1
where MIN is a function that equals the lesser of the two values in curly brackets (or that equals each of these two values if they are the same), k is a non-negative integer that here equals the number of race entrants, and the Greek letters Δ and γ are non-negative real numbers[33] having values between 0 and 1.[34]
With these parameters, we can calculate the expected net payoff Ek to the kth potential entrant from entering the race at the time when the kth potential entrant decides to enter the race. The overall probability that someone will win the race if the kth potential entrant enters (but before anyone else enters) is Pk = MIN{[γ + k∙Δ], 1}. Because each entrant is assumed to have an equal chance of winning the race, the chance that the kth potential entrant will win if it enters is Pk/k. Furthermore, because the reward from winning is V, the kth potential entrant’s expected reward from entering the race is the product of this probability of winning and the reward from winning: (Pk/k)V. The kth potential entrant’s expected net payoff Ek is this expected reward minus the cost Ck of participating in the race:
Ek = (Pk/k)V – C.
Under the model’s rational profit-maximizer assumption (with an arbitrary tie-breaker in favor of entering the race), the kth potential entrant is expected to enter the race as long as the expected net payoff is greater than or equal to zero:[35] i.e., Ek ≥ 0 or, equivalently, for Pk/k ≥ f.
The kth potential entrant will not enter the race if Ek < 0, which will occur if Pk/k < f: i.e., if at least one of γ/k + Δ or 1/k is less than f. The result is that the race will have a finite number of expected entrants n, the maximum number for whom participation in the race has a positive expected value. The number n is greater than 0 if P1 ≥ f: i.e., if γ + Δ ≥ f.
To simplify the ensuing discussion, assume that n∙Δ is small enough relative to the quantity (1 – γ) that Pn = γ + n∙Δ ≤ 1. This assumption avoids the need to take into account the “kink” in the equation Pk = MIN{[γ + k∙Δ], 1}, through which Pk transitions from a linearly increasing function of k to a constant of 1. With this simplifying assumption, we can derive the number n of expected race participants by temporarily replacing the integer variable k in the equation for Ek with a more general real-number variable K. Then, the non-negative value of K for which EK = 0 is given by the following equation:
K0 = γ/(f – Δ).
The number n of expected race participants is the largest non-negative integer less than or equal to K0:
n = INT(K0)
where the “INT” function rounds a real number to its integer part (e.g., INT(3.9) = 3).
In short, this subpart’s model yields an expected number of race participants based on three non-negative parameters: γ, Δ, and f. Two of these parameters relate to the probability of the relevant patentable innovation’s being developed if there are k participants in the race: Pk = γ + k∙Δ is the probability of the innovation’s being developed if there are k participants in the race and Pk ≤ 1. The third parameter f is the ratio between the individual cost of participating in the race and the reward obtained by an individual participant for winning the race: f = C/V.
A final question is how to relate this model to overall social welfare. The goal for society is assumed herein to be one of maximizing social welfare. If, outside effects from changes in the probability of developing the innovation and the effects of entry on race participants’ individual chances of winning, there are no positive or negative externalities that change with the number of race participants and if the development of the relevant innovation produces a positive value U for society as a whole (including the winner of the race),[36] the expected net value to society Wk from a race with n expected participants is zero for n = 0 and given by the following formula for n ≥ 1:
Wn = Pn∙U – n∙C.
Under our assumptions, society gains from having any nonzero number of participants in the innovation race: Wn > 0 for n ≥ 1 because we know from the preceding that, for n ≥ 1, En = (Pn/n)V – C ≥ 0 and thus (Pn∙V – n∙C) ≥ 0.
On the other hand, from society’s perspective, the optimal number of participants in the innovation race can be less than n. This is seen by observing how the value of the social welfare Wk changes when k is increased by 1 relative to any value of k ≥ 1:
Wk+1 – Wk = Δ∙U – C.
If Δ∙U – C > 0, society benefits from having the maximal number of participants in the race. On the other hand, if Δ∙U – C < 0, the addition of any race participants after the first participant actually decreases overall social welfare even if that addition raises the probability of overall success in developing the innovation. This is the familiar phenomenon of social-value dissipation from private-interest-motivated racing,[37] to which relatively early grants of broad patent rights have been argued to be a potential solution.[38]
A takeaway for the concern of diversion from higher-value innovation efforts that might result from comparatively low patentability standards is that such diversion might actually be desirable if, from society’s perspective, there would otherwise be a greater than optimal number of individuals pursuing higher-value innovation. Maximizing the number of participants in a patent race is not always socially desirable.[39] Relatedly, one might expect that sometimes the social value from adding a participant to a lower-level innovation race might be greater than that expected from adding a participant to a higher-level innovation race, thereby mitigating the diversion concern that our patent-racing model is meant to help explore. The next subpart explores this and other possibilities relating to the diversion concern.
B. Two-Tiered Racing Model Showing Limited Diversion
To investigate the diversion concern, we now assume that there will be a limited number of investments, each of cost C, in innovation and give each of the prospective investors a choice of investing C in either (1) lower-level innovation efforts associated with relatively high values for P1 or (2) higher-level innovation efforts associated with relatively low values for P1.[40] These characteristics of lower-level innovation and higher-level innovation are posited to correspond to patentability standards—at least in the form of the nonobviousness standard—because judicial instruction on assessment of nonobviousness explicitly references concerns of how predictable an innovation is[41] or whether, at the relevant time, there was “a reasonable expectation of success” in assembling different aspects of prior art to generate it.[42] Thus, the notion that there are general correspondences between “relative patentability” and probabilities of success in pursuing an innovation seems reasonably plausible.
Under a utilitarian view, if we are concerned about an overly liberal patent system’s generating a potential diversion of effort from higher-level innovation to lower-level innovation, it is presumably because we expect that higher-level innovation efforts that might be abandoned are anticipated, on average, to generate greater expected social value than lower-level innovation efforts that substitute for them. This expectation might reflect a suspicion that relatively higher-probability-of-success lower-level innovation is significantly more likely to be successfully developed in the absence of the patent system than higher-level innovation and thus that undertaking the costs of patent protection is less likely to be socially justified to help stimulate such innovation.[43] Alternatively, the expectation might reflect a sense that the more nonobvious an innovation—the greater its leap forward from the prior art—the more its development and disclosure through the patent system is likely to have a “positive multiplier” effect on social knowledge and practice.[44]
In investigating the diversion concern, a preliminary question is whether the patent system is likely to lead to a proportionately greater appropriation of public value by a private developer of higher-level innovation than by a private developer of lower-level innovation. If the answer is “Yes,” then the diversion concern might be satisfactorily answered by pointing to this tendency of the patent system to favor higher-level innovation. At the very
least, this tendency would seem likely to substantially mitigate a concern that, through relatively low patentability standards, the patent system could be problematically diverting effort to lower-level innovation.
If the answer is “No”—i.e., that there is no general reason to expect higher private appropriability of the social value of higher-value innovation—then there are two remaining possibilities. First, if patents tend to give disproportionately large private rewards to lower-level innovators, then there is relatively little need to use a two-tiered patent-racing model to conclude that there is likely a substantial problem with the incentives provided by the patent system. In order to effectively harness private incentives in a way that best serves society’s interests, those incentives should be appropriately proportioned to the social value that private activities are expected to contribute. If recalibration of patent scope or remedies to reduce excessive awards for lower-level innovation or to increase deficient awards for higher-level innovation is either impossible or otherwise problematic, raising patentability standards to avoid distortions from those excessive awards might be society’s best option.
For purposes of this Essay’s two-tiered patent-racing model, the scenario of most interest is the last one: a scenario in which the private appropriability of social value from innovation is substantially the same for lower-level and higher-level innovation. Thus, the remainder of this subpart assumes this scenario. In the symbology of the preceding subpart, this scenario is one in which U/V, the ratio between the social value of an innovation and the private value captured by the race winner, is substantially the same for lower-level and higher-level innovation.
Returning to the symbology of subpart II(A), let us assume there are two forms of innovations, a lower-level and a higher-level innovation, in which parties can invest the cost of entering an innovation race C. For purposes of notational simplicity, I will hereinafter refer to the lower‑level innovation as the “Small” innovation, associated with the index symbol “S”; and the higher-level innovation as the “Big” innovation, associated with the index symbol “B.” In this context, the diversion question is whether making patents available for the Small innovation will undesirably compromise investment in the Big innovation. The probability of success in developing the Small innovation is relatively substantial even when only a single party invests C to pursue the innovation. For the Big innovation, in contrast, a one-party innovative effort has a comparatively low probability of success, but both the private and social utility gain from successful development of the Big innovation is large compared to that from successful development of the
Small innovation. Such points can be summarized by a series of inequalities that use a modified version of the symbology of subpart II(A):
PS1 >> PB1
VB >> VS
UB >> US
where the “B” and “S” subscripts associate the relevant parameters with the Big and Small innovations, respectively, and where the symbol “>>” indicates that the quantity to the left is substantially greater than the quantity to the right. In contrast to these substantial inequalities, we have previously indicated that, in situations of concern here, the patent system renders the private appropriability of the value of the relevant innovations about the same: UB/VB ≈ US/VS, where “≈” indicates approximate equivalence.
Following subpart II(A), the private expectation values for being the kth entrant into a race for the Big or Small innovation are expressed, respectively, as follows:
EBk = (PBk/k)VB – C
ESj = (PSj/j)VS – C
where
PBk = γB + k∙ΔB
PSj = γS + j∙ΔS.
Because the Big innovation is a comparatively low-probability innovation, one can reasonably posit that additional participants after the first are likely to add more to the overall probability of success in a race to develop the Big innovation than they do for the Small innovation. For starters, there is more room to raise the overall probability of success because PS1 >> PB1.[45] Moreover, the comparatively low probability of individual success in developing the Big innovation seems likely to correlate with greater uncertainty about how to proceed in developing the innovation. By exploring relatively plausible alternative paths to the innovation, secondary participants in the Big innovation race thus might be expected to add more to the likely success of the overall effort than with respect to Small innovation for which paths of development seem likely, on average, to be more predictable and perhaps even well-trod. In short, the increment ΔB to the overall probability of success in developing the Big innovation from adding a participant to its
race may be reasonably assumed to be substantially greater than the corresponding increment ΔS for the Small innovation race:
ΔB >> ΔS.
A corollary of this assumption and the earlier assumption that VB >> VS is that
ΔB∙VB >> ΔS∙VS.
Further, the relatively high value assumed for PS1 and the sense that the Small innovation is likely to be more predictable suggest that we can also assume that PS1 >> ΔS.
The diversion question for UB/VB ≈ US/VS now essentially boils down to questions of (1) whether and when a would-be innovator chooses to invest in pursuing the Small innovation rather than pursuing the Big innovation; and (2) whether we think there is a social loss from the would-be innovator’s choosing the Small innovation race if and when that happens. The short answer is that diversion is certainly possible but that it also turns out to be a relatively limited and contained concern. Generally speaking, pursuit of the Big innovation is reasonably strongly prioritized when, from a social welfare standpoint, it most should be. The prospect of likely undesirable diversion of investment toward Small innovation seems likely to occur only in situations where the differences in relevant parameters between the Big and Small innovation are only relatively marginal (with diversion thus being a less significant concern from the get-go) or there is already significant investment in the Big innovation, perhaps enough that further investment in the Big innovation is not likely to add much net social value in any event.
Figure 1: The top graph shows values of EBk + C in units of VS for γB = ΔB = 0.05 and VB = 6VS. The bottom graph shows values of ESj + C in units in units of VS for γS = 0.4 and ΔS = 0.01. Note that only one value of ESj + C—namely, ES1 + C —exceeds any of the values of EBk + C.
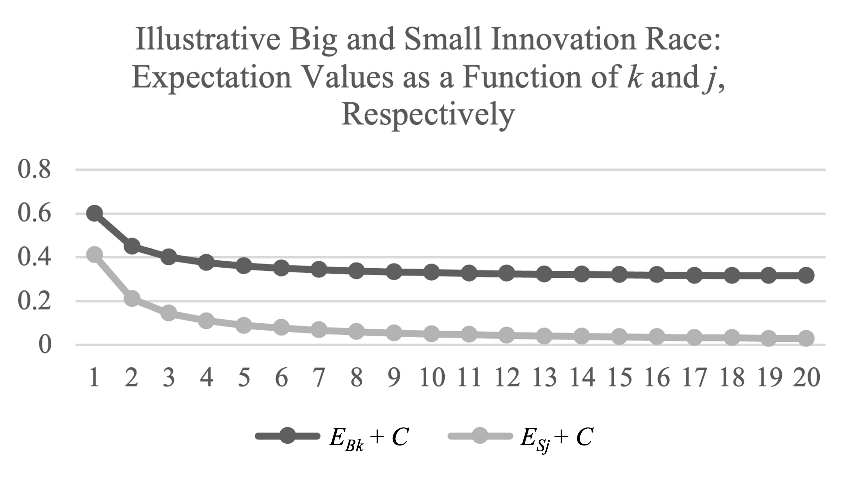
Figure 1 illustrates key bases for the sense that diversion from higher-level innovation to lower-level innovation is likely to be reasonably well contained for UB/VB ≈ US/VS. Figure 1 shows versions of EBk and ESj as functions of k and j, respectively. As indicated in the caption for Figure 1, for the parameter values assumed, only one value of ESj—specifically, ES1—exceeds any of the values of EBk. Further, the resulting potential “diversion” one innovation investment to Small innovation results in is likely to be socially desirable in any event. That investment is likely to generate more social value from the investment C than investing the amount C in a Big innovation race that would then involve three or more participants.
To see the basis for Figure 1’s graphs and this conclusion, it is helpful to rewrite the equations for EBk and ESj by replacing PBk and PSj with the right sides of the formulas PBk = γB + k∙ΔB and PSj = γS + j∙ΔS. After dividing these expanded numerators by k and j respectively, one obtains:
EBk = γB∙VB/k + (ΔB∙VB – C)
ESj = γS∙VS/j + (ΔS∙VS – C).
These equations make clear that, as modeled, the expectation values for being the kth and jth participants in the Big and Small innovation races vary with k and j as 1/k and 1/j. As k and j become larger and larger (i.e., go to infinity), the values of EBk and ESj converge from above on the constant values (ΔB∙VB – C) and (ΔS∙VS – C), respectively. Consequently, EBk is greater than (ΔB∙VB – C) for any finite value of k. Meanwhile, the maximum value for ESj occurs when j = 1. In other words, the maximum value for ESj is ES1 = PS1∙VS – C = γS∙VS + ΔS∙VS – C. If the quantity (ΔB∙VB – C) is greater than or equal to ES1—i.e., if ΔB∙VB ≥ PS1∙VS—EBk is greater than ESj for any finite values of k and j. When ΔB∙VB ≥ PS1∙VS, there is no mth investor for any finite number m who will prefer investing in the Small innovation over investing in the Big innovation.
In short, if the product ΔB∙VB is greater than or equal to PS1∙VS, there is no point (short of infinity) at which a would-be investor prefers to invest in the Small innovation over the Big innovation, and there is thus no problem with diversion to the Small innovation. For ΔB > 0, one can restate this condition for no diversion as a condition that the ratio VB/VS be greater than PS1/ΔB. Hence, for Big innovations presumed to be of most importance to society—i.e., for Big innovations of truly transcendent value such that VB/VS is much, much greater than 1—diversion to a lower-value Small innovation is not likely to be a concern as the high VB/VS ratio means that ΔB∙VB is likely to be large enough relative to PS1∙VS to ensure that all rational investments go to pursuit of the Big innovation.
What about situations where ΔB∙VB < PS1∙VS? In these situations, there might be diversion from the Big innovation to the Small innovation. But there is also a strong possibility that this diversion is no more than a second-order concern and perhaps even socially desirable.
A first point is that, as long as PB1∙VB is greater than PS1∙VS, the first investment will go to the Big innovation. Within our model, the relation PB1∙VB > PS1∙VS means that the expectation value of being the first participant in the Big innovation race, EB1, is greater than the expectation value of being the first participant in the Small innovation race, ES1.
Moreover, under the assumption that UB/VB ≈ US/VS, deviation from the condition that PB1∙VB > PS1∙VS means that prioritizing initial investment in the Small innovation is reasonably likely to be socially desirable. Under conditions where UB/VB ≈ US/VS and PB1∙VB ≤ PS1∙VS, the expected overall social benefit from a first investment in the Big innovation, PB1∙UB, is reasonably likely to be less than the expected social benefit from a first investment in the Small innovation, PS1∙US. Further, because the amount to be invested is the same for either form of innovation, the bottom line for society might well be that the expected increase to social welfare from directing the first investment to the Small innovation is greater than the expected increase to social welfare if that investment were instead directed to the Big innovation. In short, when PB1∙VB ≤ PS1∙VS, “diversion” of the first investment to the Small innovation might be precisely what is desired.[46]
There is a possibility, however, that when PB1∙VB ≤ PS1∙VS, diversion of investment to the Small innovation could extend beyond the first investment. But this tends to be a limited concern because of the 1/j dependence of ESj = γS∙VS/j + (ΔS∙VS – C). As indicated by Figure 1 (albeit in an overall scenario in which PB1∙VB > PS1∙VS), such 1/j dependence drives ESj toward (ΔS∙VS – C) and thus toward a value less than any value of EBk, which has a floor of (ΔB∙VB – C). Consequently, the diversion concern is essentially doubly self-limiting, only arising sharply in circumstances where two conditions apply: (1) the social value of the Big innovation is not so transcendent that it and its privately appropriated portion counterbalance the relatively low probability of success in developing it; and (2) there is not enough investment available to enable the value of investing in the Big innovation to become dominant because of ESj’s convergence to (ΔS∙VS – C).
A similar point applies for the possibility that secondary or later investments will go to the Small innovation when PB1∙VB is greater than PS1∙VS, a starting situation that corresponds more precisely to Figure 1. For PB1∙VB > PS1∙VS, the first investment will, as already noted, go to the Big innovation. Moreover, if the second investment goes to Small innovation, that might well be socially desirable. If a second or later investment is rationally invested in the Small innovation, that means that ES1 ≥ EBk for k ≥ 2, which in turn means that PS1∙VS ≥ (γB/k + ΔB)VB and thus that PS1∙VS ≥ ΔB∙VB. For UB/VB ≈ US/VS, this in turn means that the expected social welfare gain from the first investment in the Small innovation, PS1∙US, is reasonably likely to be greater than the expected social welfare gain from additional investment in the Big innovation, ΔB∙UB. In short, there is a very good chance that the increment from making a first investment in the Small innovation is socially preferable to further investment in the Big innovation.
More generally, where PB1∙VB > PS1∙VS, any diversion to the Small innovation is strictly limited in the sense that, no matter the number of investments, at least half of all investments will go to the Big innovation. Recall that ΔB∙VB >> ΔS∙VS. Now consider the two alternative subsets of circumstances where γB∙VB > γS∙VS and where γB∙VB ≤ γS∙VS. Where γB∙VB > γS∙VS, a straightforward result of the equations for EBk and ESj is that EBk > ESk for all k ≥ 1. In other words, under the rational-profit-maximizer assumption, the kth investment in the Small innovation will never occur until after the kth investment in the Big innovation. Thus, there can never be more invested in the Small innovation than in the Big innovation. The same is true for γB∙VB ≤ γS∙VS, although here the proof is more involved.[47]
In short, this subpart’s two-tiered patent-racing model for innovation suggests that diversion from higher-level patentable innovation to lower‑level patentable innovation is possible but also of self-limiting concern in circumstances where the patent system’s implicit assumptions about the utility of harnessing private interest to promote social welfare hold—namely, where the private appropriability of social value from innovation is substantially similar across higher-level and lower-level forms of innovation. True, even under this model and its treatment here—involving various assumptions favorable to the patent system—there can be—indeed is likely to be—some socially undesirable diversion of effort to lower-level innovation in a patent system with markedly low patentability requirements. Moreover, in a world in which there are many Small innovations that could be targeted for development, such diversion concerns might multiply accordingly. Thus, if one expects or demands a great degree of perfection from the patent system in its operation to promote scientific and technological progress, one might view the behavior patterns predicted by the model as alarming, rather than at least mildly comforting.
My starting point, however, is a view that the patent system is fundamentally a relatively crude social instrument for promoting scientific and technological progress.[48] Hence, in light of this view of the patent system’s fundamental nature, the suboptimality in its operation that the model suggests seems insufficient to declare the system to fail a self‑consistency test. At least when the focus is potential diversion from a higher‑level patentable innovation to a lower-level patentable innovation and when it is true that the private appropriability of social value from the higher-level innovation is not substantially lower than that of social value from the lower‑level innovation, the system appears to perform reasonably well relative to the level of imperfection that is more facially baked into its operation.
C. Extra-System Diversion Concerns Contrasted
The analysis of the preceding subpart does not explicitly address concerns about potential diversion of effort from a “Big” but non-patentable innovation to a “Small” but patentable innovation. One can straightforwardly extend the analysis of subpart II(B) to such “extra-system” diversion concerns if one assumes a mechanism for appropriating value from non‑patentable innovation that is similarly likely to support an innovation race. More generally, however, concerns about potential extra-system diversion are not self-consistency concerns—i.e., are not concerns about the extent to which the patent system could undermine itself—and thus are substantially beyond the scope of this Essay. As in the case of previously flagged concerns about potentially disproportionate appropriability for lower-level innovation, however, society might generally benefit from efforts to establish incentive systems for innovation that provide rewards of reasonably consistent proportion to innovation’s expected social value.[49]
D. Patent Blocking as Threat for Cumulative Innovation
In contrast to the two-tiered patent-racing model’s suggestion that intra‑system diversion will commonly be a problem of limited scope, there is little such reassurance in relation to concerns of patent blocking. Under the model, the capacity of a patent on Small innovation to eat into the expected private value of the Big innovation VB means that blocking patents on the Small innovation can dramatically and consistently undercut incentives to invest in the Big innovation even if there are substantial funds available in principle for such investment. Blocking patents can cut into the value of winning a Big innovation race in much the same way that an additional entrant in the race for a Big innovation does: by taking a direct cut out of the expected value of investing in the Big innovation. If Small innovation patents undercut the value of VB to the extent that PB1∙VB – C < 0, investment in higher-level innovation never gets off the ground.
There are other situations in which the patent-blocking concern is likely to be especially sharp. Where the relevant Small innovation is likely to be developed in any event as part of the pursuit of the Big innovation, there can be a question whether offering a patent for the Small innovation has added anything substantial to social welfare, and any undercutting of incentives to pursue the Big innovation can be particularly nettlesome. In other situations, the Big innovation might have ended up incorporating a patented Small innovation unnecessarily and only as a matter of chance and thus might have failed to benefit in any substantial way from separate development of the Small innovation despite having to pay for it through ex post licensing, settlement, court-ordered remedies, or a now costly switch to an alternative component technology.[50]
Blocking concerns appear more likely to be amenable to judicial or political mitigation than diversion concerns, however. Courts can mitigate blocking concerns by making clear their intent to restrict remedies for inadvertent infringement of Small innovation patents by a Big innovation. At least arguably, courts have, in the past two decades, made such mitigation more readily available by becoming more willing to deny patentees’ petitions for injunctive relief[51] and by emphasizing proper limits on the size of awards of patent-infringement damages.[52] Rejection of overly “rigid” demands for challenges to nonobviousness[53] and revitalization of subject-matter eligibility doctrine to block or undo the effective patenting of very broadly applicable but substantially conventional “abstract ideas”[54] might be viewed as illustrating an alternative response to concerns about overly taxing patents on Small innovation: an effort at an at least incremental raising of patentability standards.[55]
Conclusion
This Essay has used a two-tiered patent-racing model to explore the dangers of socially undesirable diversion of investment or patent blocking from U.S. patent law’s liberal approach to patentability standards—i.e., the patent system’s use of patentability standards that predictably permit the patenting of relatively low-level innovation. Analysis of the model’s operation suggests that, at least under assumptions that appear to generally underlie presumptions of patent-system efficacy, the blocking concern might often be the greater worry.[56]
The patent-racing model helps alleviate somewhat concerns that low patentability standards might lead to a substantial diversion of effort from more socially desirable investments in higher-level innovation to less socially desirable investments in lower-level innovation.[57] To be sure, if the patent system enables lower-level innovators to appropriate substantially greater proportions of the social value of their innovations than higher-level innovators can appropriate from the social value of their innovations, diversion should be a matter of significant concern.[58] In relation to diversion, the main novel point here is that, if instead the patent system generally succeeds in rewarding innovators with relatively consistent fractions of the social value that their innovations generate, diversion concerns can be substantially limited in scope.[59] This conclusion results substantially because, within the model, a base contribution to the probability of winning a patent race falls to zero as the number of the participants increases, and a constant contribution to the probability of winning appears reasonably likely to be substantially greater for higher-level innovation than for lower-level innovation.[60] In contrast, in cumulative-innovation contexts, blocking patents on lower-level innovation can be expected commonly to undercut incentives to invest in higher-level innovation under any model in which profit incentives drive investment in higher-level innovation.[61]
There might be solace in a sense that failings of the patent system might often lie more in patent blocking than in intra-system diversion. Through limiting patent-infringement remedies and tightening patentability standards, courts can respond to plaints of higher-level innovators accused of infringement by mitigating patent-blocking dangers.[62] With respect to diversion, there seems less chance that there will be specific parties who will appear before a court with Article III standing[63] and sufficient interest and legal basis to move courts to help correct for investments that have not happened or will not happen. Complainants about diversion could try their luck with the political branches, but success in lobbying for change based on a charge of comparatively excessive incentives for lower-level innovation is likely to be handicapped not only by the difficulty of proving a counterfactual (the higher-level innovation investments and resulting social benefits that would otherwise occur) but also by the possibility that the greater weight of lobbying interests will lie with innovation efforts that are being made rather than those not being made.
In sum, this Essay’s investigation comports with a notion that, at least if the patent system generally provides private incentives of substantially consistent proportion to social welfare gains, intra-system diversion concerns might well be substantially contained whereas blocking concerns can be mitigated through government action. The Essay thus leaves room for a qualified hope that, however otherwise imperfect, the patent system might avoid the fate of the ouroboros, a serpent that eats its own tail.
- . See, e.g., John M. Golden, F. Scott Kieff, Pauline Newman & Henry E. Smith, Principles of Patent Law: Cases and Materials 35 (8th ed. 2024) (“The patent system provides incentives for several forms of innovation-related activity.”). ↑
- . See, e.g., id. at 30 (explaining how, by restricting access to a consumer good, a “monopoly regime” can generate “a deadweight loss”: “a net decrease in combined societal wealth” “relative to a perfectly competitive market”). ↑
- . See Mayo Collaborative Servs. v. Prometheus Lab’ys, Inc., 566 U.S. 66, 92 (2012) (observing that patent rights’ “very exclusivity can impede the flow of information that might permit, indeed spur, invention”). ↑
- . See Richard A. Epstein, Simple Rules for a Complex World 34 (1995) (“The basic trade-off between administrative costs and improved incentives for private behavior is always with us.”). ↑
- . Festo Corp. v. Shoketsu Kinzoku Kogyo Kabushiki Co., 535 U.S. 722, 731 (2002); see also, e.g., Ass’n for Molecular Pathology v. Myriad Genetics, Inc., 569 U.S. 576, 590 (2013) (“As we have recognized before, patent protection strikes a delicate balance . . . ”). ↑
- . Letter from Thomas Jefferson to Isaac McPherson (Aug. 13, 1813), in 6 The Writings of Thomas Jefferson 175, 181 (H.A. Washington ed., 1854). ↑
- . See infra text accompanying notes 21–27. ↑
- . See infra text accompanying note 12. ↑
- . See infra text accompanying notes 21–27. ↑
- . See Robert P. Merges & Richard R. Nelson, On the Complex Economics of Patent Scope, 90 Colum. L. Rev. 839, 881 (1990) (observing that, “in a number of technologies,” “technical advance is cumulative, in the sense that today’s advances build on and interact with many other features of existing technology”). ↑
- . 35 U.S.C. § 154(a)(1)–(2). ↑
- . See Golden et al., supra note 1, at 854 (“The Patent Act . . . provides for patent term extensions under various circumstances.”). ↑
- . See Mark Schankerman, How Valuable Is Patent Protection? Estimates by Technology Field, 29 RAND J. Econ. 77, 79 (1998) (“The distribution of the private value of patent rights is sharply skewed in all technology fields, with most of the value concentrated in a relatively small number of patents in the tail of the distribution.”). ↑
- . See, e.g., Rebecca Robbins, How a Drug Company Made $114 Billion by Gaming the U.S. Patent System, N.Y. Times (Jan. 28, 2023), https://www.nytimes.com/2023/01/28/business/humira-abbvie-monopoly.html [https://perma.cc/2N8E-4G37] (“One analysis found that Medicare, which in 2020 covered the cost of Humira for 42,000 patients, spent $2.2 billion more on the drug from 2016 to 2019 than it would have if competitors had been allowed to start selling their drugs promptly.”). ↑
- . See John M. Golden, Proliferating Patents and Patent Law’s “Cost Disease”, 51 Hous. L. Rev. 455, 476 (2013) (“The continual acceleration of patenting rates strains both public and private actors’ capacities to perform all the various activities necessary for a patent system to function effectively.”). ↑
- . See Christina Mulligan & Timothy B. Lee, Scaling the Patent System, 68 N.Y.U. Ann. Surv. Am. L. 289, 291–92 (2012) (discussing costs of patent clearance). ↑
- . U.S. Pat. & Trademark Off., FY 2022 Workload Tables, tbl.6, https://www.uspto.gov/about-us/performance-and-planning/uspto-annual-reports [https://perma .cc/6E8C-5RUU]. ↑
- . World Intell. Prop. Org., WIPO IP Facts and Figures 2022, at 8 (2022), https://www.wipo.int/edocs/pubdocs/en/wipo-pub-943-2022-en-wipo-ip-facts-and-figures-2022.pdf [https://perma.cc/7JH5-KAG7] (reporting that about 16.5 million patents were in force worldwide in 2021: 3.6 million in China, 3.3 million in the United States, and 2 million in Japan). ↑
- . See William F. Lee & A. Douglas Melamed, Breaking the Vicious Cycle of Patent Damages, 101 Cornell L. Rev. 385, 389, 405 (2016) (“Several factors often combine to make wholesale preclearance infeasible: high search costs, high negotiation costs, and high costs of delay.”). ↑
- . U.S. Const. art. I, § 8, cl. 8. ↑
- . See Fed. Trade Comm’n, To Promote Innovation: The Proper Balance of Competition and Patent Law and Policy, ch. 1, at 5 (2003) (“To obtain a patent, an invention (that is, a product, process, machine, or composition of matter) must be novel, nonobvious, and useful, and must meet certain requirements for the description of the invention.”). ↑
- . See Golden et al., supra note 1, at 71 (observing Story’s conclusion that “a patentee did not need to prove, for example, that his claimed invention of a water pump is ‘a better pump than the common pump’” (quoting Lowell v. Lewis, 15 F. Cas. 1018, 1019 (C.C.D. Mass. 1817))). In the early decades of U.S. patent law, there was greater willingness to consider “whether the social benefits of a particular invention justified a patent.” Oren Bracha, Owning Ideas: The Intellectual Origins of American Intellectual Property, 1790–1909, at 204 (2016). But U.S. courts have decisively shifted toward viewing the utility requirement “as a minimum threshold requirement, and a very low threshold at that.” Andrew C. Michaels, Benefits of the Invention and Social Value in Patent Law, 29 Geo. Mason L. Rev. 827, 836 (2022). ↑
- . See HTC Corp. v. Cellular Commc’ns Equip., LLC, 877 F.3d 1361, 1368 (Fed. Cir. 2017) (“A claim is anticipated [a.k.a. lacking novelty] if a single prior art reference discloses all the claimed limitations arranged or combined in the same way as in the claim.” (citation omitted)). ↑
- . See Golden et al., supra note 1, at 549–50 (describing disclosure requirements). ↑
- . See, e.g., Bilski v. Kappos, 561 U.S. 593, 606 (2010) (declaring that the Court’s opinion on subject-matter eligibility contains “[n]othing [that] should be read to take a position on where [the] balance ought to be struck” “between protecting inventors and not granting monopolies over procedures that others would discover by independent, creative application of general principles”). ↑
- . Giles S. Rich, Laying the Ghost of the “Invention” Requirement, 1 AIPLA Q.J. 26, 27–34 (1972) (describing the nonobviousness standard as “restrict[ing] the courts in their arbitrary . . . judgments on patentability” and helping “[t]o prevent the use of too high a standard”). ↑
- . See Golden et al., supra note 1, at 381 (“[T]he claimed invention must be significantly different, not necessarily better . . . ”). ↑
- . Gideon Parchomovsky, Publish or Perish, 98 Mich. L. Rev. 926, 926 (2000) (describing the standard patent “race model” as “assum[ing] that the winner, namely the first to invent, takes the patent grant with the market dominance that comes with it”). ↑
- . Alternatively, one could view each entrant as gaining the same amount (e.g., some additional know-how) from participating in the race, but with this universal gain taken into account by discounting it from the entrant’s cost of racing. ↑
- . Cf. John F. Duffy, Rethinking the Prospect Theory of Patents, 71 U. Chi. L. Rev. 439, 473 (2004) (describing a model that uses this equal-cost assumption). ↑
- . The assumptions of a winner-take-all race in which entrants have equal chances of winning are common in patent-racing literature. See, e.g., Partha Dasgupta & Joseph Stiglitz, Uncertainty, Industrial Structure, and the Speed of R&D, 11 Bell J. Econ. 1, 18 (1980) (describing a patent-racing model in which, with n entrants, “each entrant receives either the entire benefit or nothing, but his expected gain is just 1/nth the value of the patent”). ↑
- . The symbol “∙” immediately after f indicates multiplication—i.e., “f∙V” is the product f times V. ↑
- . The first entrant, corresponding to k = 1, thus adds at least as much to the overall probability of developmental success as any later entrant: γ + Δ ≥ Δ. Even if a later entrant is equally competent in pursuing the innovation when compared to the first and there is no duplicativeness to their efforts, a later entrant can commonly be expected to add less to the overall probability of success than the first simply because the probability of success is not zero without the later entrant. For example, if each of two potential entrants has a 50% probability of successfully developing an innovation and these probabilities are independent of one another, the probability of successful development is 50% if one of them enters the race but only increases to 75% if both of them enter the race (the probability of neither of them developing the innovation being one-half times one-half or 25%). ↑
- . For simplicity, the value Δ is assumed constant. More realistically, Δ might be expected to be a decreasing function of k for the same reason that we might expect the first entrant to add to the overall probability of success more than later entrants do. See supra note 33. A further reason for such decrease could be that, at least in the large-k limit, limits on imagination, resources to support innovation efforts, or even on the range of potential plausible approaches to developing a particular innovation will likely mean that there are diminishing or even vanishing returns from the further addition of even equally capable innovation-race participants (presuming they are even available). Substituting for constant Δ a function Δ(k) that is a decreasing function of k is not expected, however, to affect the qualitative observations discussed in this Essay given that a key starting point in subpart II(B) is an assumption that Δ(1) for higher-level innovation is much larger than Δ(1) for lower-level innovation and, with respect to a race with n entrants, the equation for Ek means that the level of incentive for the nth (i.e., marginal) entrant would reflect the average value of Δ(1) through Δ(n), rather than merely Δ(n) by itself. ↑
- . Cf. Duffy, supra note 30, at 472–73 (discussing how a firm decides whether to join a patent race). ↑
- . Of course, innovations and innovation processes can in principle have negative effects on social welfare. A modern society mindful of the risks, for example, of nuclear holocaust or a human‑generated pandemic, is well aware of this. For purposes here, however, it can be assumed that either a general tendency to have positive private values correspond with positive public values or other policy mechanisms, such as regulatory law and ethical codes, suffice to render reasonable an assumption that the social welfare effects of innovations with which the patent system are concerned are generally positive. This assumption might be even more reasonable if the patent system itself required positive social utility as a condition of patentability. United States patent law is, however, generally understood to feature no significant requirement of moral or beneficial utility. See John M. Golden, Stem Cell Patents in the United States, in Research Handbook on Intellectual Property and the Life Sciences 243, 254 (Duncan Matthews & Herbert Zech eds., 2017) (observing that, in U.S. patent law, “any requirement of ‘beneficial utility’ has retreated to essential insignificance” (footnotes omitted)). ↑
- . See John M. Golden, Principles for Patent Remedies, 88 Texas L. Rev. 505, 530 (2010) (noting that “a patent race . . . can generate socially inefficient levels of investment because, in such a race, the private and social values of additional investment can substantially diverge” (footnote omitted)). ↑
- . See Duffy, supra note 30, at 509–10 (noting a classic argument that “[t]he early grant of rights would put an end to patent racing and therefore lead to more efficient development of the [patented] technology” and the added point that the resulting “earlier termination of the rights” can helpfully serve as the primary mechanism by which “patent rents are dissipated”). ↑
- . See William M. Landes & Richard A. Posner, The Economic Structure of Intellectual Property Law 300–01 (2003) (“Such a race can generate costs of invention that exceed the social benefits, because the first competitor to reach the finish line will obtain the patent [and associated reward] even if he beat his competitors by only a day.” (footnote omitted)). ↑
- . In practice, of course, investments in individual innovation efforts need not be the same size, perhaps particularly when some of the innovation efforts are in pursuit of higher-level innovation and some are in pursuit of lower-level innovation. The notion of a single investment size C is meant to simplify exposition but, as the key point for rationally profit-maximizing investors will be the return on investment, the simplification is not thought likely to affect first-order results, particularly given the risk-neutrality and discrete probabilities of success already assumed by the patent-racing model. ↑
- . See KSR Int’l Co. v. Teleflex Inc., 550 U.S. 398, 416 (2007) (“The combination of familiar elements according to known methods is likely to be obvious when it does no more than yield predictable results.”). ↑
- . Orexo AB v. Actavis Elizabeth LLC, 903 F.3d 1265, 1271 (Fed. Cir. 2018). ↑
- . Cf. Michael Abramowicz & John F. Duffy, The Inducement Standard of Patentability, 120 Yale L.J. 1590, 1593–94 (2011) (contending that “if [an] innovation would be created and disclosed even without patent protection, denying a patent on the innovation costs society nothing . . . and saves society from needlessly suffering the well-known negative consequences of patents”). ↑
- . Cf. Duffy, supra note 30, at 504 (“[T]he innovation for which society is conferring [a patent] must be of sufficient importance that significant positive externalities do exist.”). ↑
- . This can be viewed as a generalization of earlier reasoning about why P1 can often be expected to be greater than Δ. See supra note 33. ↑
- . This conclusion corresponds with the fact that in the limit where PB1 approaches zero (which implies also that ΔB approaches zero), investment in pursuit of the Big innovation becomes fundamentally wasteful. Plowing valuable social resources into pursuit of a grand but presently hopeless dream might capture the imagination but seems unlikely to be the best way to advance social welfare.Admittedly, in a world shorn of the simplifying assumptions of our model, there might be serendipitous discoveries or other intermediate or tributary advances that result from an innovative effort. The probability of such results and their expected utilities could then be added to the calculation of which course is best to pursue. But the possibilities of such secondary benefits should then also be added to the potential results of pursuing Small innovation. Further, one might consider whether there is social value in a potentially more “democratic” aspect to Small innovation efforts: engagement in these might often be more accessible in the sense that Small innovation is more likely to be realistically pursued by a larger swath of potential innovators and investors. In the end, I close with an intuition that if PB1∙VB ≤ PS1∙VS, diversion of some significant innovative investment to Small innovation might well be socially desirable for UB/VB ≈ US/VS. ↑
- . The proof can be achieved using mathematical induction. Start by assuming that EBk > ESk for some k. We can derive from the equations for EBk and ESk that EBk = EB(k+1) + γB∙VB[1/k – 1/(k+1)] and ESk = ES(k+1) + γS∙VS[1/k – 1/(k+1)]. Substitution into the inequality EBk > ESk then yields the inequality EB(k+1) > ES(k+1) + (γS∙VS – γB∙VB)[1/k – 1/(k+1)]. Recall that we are here considering circumstances where γB∙VB ≤ γS∙VS. Consequently, the first quantity in parentheses in this last inequality (γS∙VS – γB∙VB) is non-negative. Further, because k ≥ 0, the quantity in brackets [1/k – 1/(k+1)] is strictly positive. Thus, the product of these two quantities (γS∙VS – γB∙VB)[1/k – 1/(k+1)] is non-negative, and the inequality EB(k+1) > ES(k+1) + (γS∙VS – γB∙VB)[1/k – 1/(k+1)] means that EB(k+1) > ES(k+1). In short, if EBk > ESk, then EB(k+1) > ES(k+1). Now recall that we are looking at situations where PB1∙VB > PS1∙VS, and thus EB1 > ES1. By mathematical induction, it follows that EBk > ESk for all k ≥ 1. See W.H. Bussey, The Origin of Mathematical Induction, 24 Am. Mathematical Monthly 199, 199–200 (1917) (describing proof by mathematical induction). ↑
- . See John M. Golden, Patent Privateers: Private Enforcement’s Historical Survivors, 26 Harv. J.L. & Tech. 545, 617 (2013) (observing that “patents for invention have historical roots that substantially coincide with those of other, largely outdated mechanisms for harnessing private enterprise to public ends”); Richard S. Markovits, On the Economic Efficiency of Using Law to Increase Research and Development: A Critique of Various Tax, Antitrust, Intellectual Property, and Tort Law Rules and Policy Proposals, 39 Harv. J. Legis. 63, 114 (2002) (pointing to various reasons for “surprise[] if our current system [for promoting innovation through intellectual property rights] did not cause substantial misallocation” of resources); Steven Shavell & Tanguy Van Ypersele, Rewards Versus Intellectual Property Rights, 44 J.L. & Econ. 525, 529 (2001) (noting that the patent system can generate both “incentives to invest in research [that] are inadequate” and “deadweight loss” from monopoly pricing). ↑
- . See supra text accompanying notes 44–45. ↑
- . See Golden, supra note 37, at 518 (“Strong patent rights might force such a ‘trapped’ party to pay a licensing fee based more on switching costs than the more intrinsic value of the patented invention.” (footnote omitted)). ↑
- . See John M. Golden, The Rise of Judicial Ratemaking in Patent Law, 38 Harv. J.L. & Tech. (forthcoming 2025) (manuscript at 3) (on file with author) (observing that “the one-two combination of the denial of a permanent injunction against continuing infringement and the ordering of a court-determined ‘ongoing royalty’ for future infringement has become an unremarkable outcome in U.S. patent litigation” (footnote omitted)). But cf. Mark P. Gergen, John M. Golden & Henry E. Smith, The Supreme Court’s Accidental Revolution? The Test for Permanent Injunctions, 112 Colum. L. Rev. 203, 205 (2012) (“rais[ing] substantial concerns about” the approach to permanent injunctions). ↑
- . See John M. Golden, Discretion in Patent Damages, 37 Rev. Litig. 287, 311 (2018) (discussing decisions of the U.S. Court of Appeals for the Federal Circuit “that overturned trial court [reasonable-royalty] awards and incrementally tightened the standards for the admissibility and sufficiency of evidence” supporting such awards (footnote omitted)). But cf. William F. Lee & Mark A. Lemley, The Broken Balance: How “Built-In Apportionment” and the Failure to Apply Daubert Have Distorted Patent Infringement Damages, 37 Harv. J.L. & Tech. 255, 262 (2024) (contending that “the Federal Circuit and district courts have been backsliding from the principle of apportionment” intended to generate properly sized damages awards). ↑
- . KSR Int’l Co. v. Teleflex Inc., 550 U.S. 398, 415 (2007) (“We begin by rejecting the rigid approach of the Court of Appeals [to analyzing obviousness].”). ↑
- . E.g., Alice Corp. Pty. Ltd. v. CLS Bank Int’l, 573 U.S. 208, 227 (2014) (rejecting as “patent-ineligible” claims that “add[ed] nothing of substance to [an] underlying abstract idea”); see also John M. Golden, Flook Says One Thing, Diehr Says Another: A Need for Housecleaning in the Law of Patentable Subject Matter, 82 Geo. Wash. L. Rev. 1765, 1768–69 (2014) (observing that, “[s]ince [2006], the [U.S.] Supreme Court has held that patent claims fail requirements of subject-matter eligibility in four straight opinions” and “judges of the Federal Circuit have begun policing limits on patentable subject matter more aggressively”). ↑
- . See supra text accompanying notes 44–45. ↑
- . See supra subpart II(D). ↑
- . See supra subpart II(B). ↑
- . See supra text accompanying notes 44–45. ↑
- . See supra text accompanying notes 47–48. ↑
- . See supra text accompanying notes 47–48. ↑
- . See supra subpart II(D). ↑
- . See supra text accompanying notes 51–56. ↑
- . See FDA v. All. for Hippocratic Med., 144 S. Ct. 1540, 1556 (2024) (“By requiring the plaintiff to show an injury in fact, Article III standing screens out plaintiffs who might have only a general legal, moral, ideological, or policy objection to a particular government action.”). ↑